by Scott Teresi
www.teresi.us/writing



        When considering the large number of variables which must be chosen with unbelievably high precision within a small moment of time to, say, hit a baseball, it appears that such a feat should be nearly impossible for all but maybe a computer which could arrive at the correct calculations within a microsecond. However, a professional baseball player, whether or not he has finished high school earning an "A" on his physics exam, can execute the task with very good relative reliability. Though baseball is not a scientific sport, as with numerous other recreational activities, principles of physics can be used to describe the behavior of its elements, ordinarily unbeknownst to its players.

        For instance, a typical major league pitcher has probably never heard of the Magnus effect, which is the principle explanation for the deflection of his curve ball. G. Magnus described why a rough spinning object traces a slightly curved trajectory. A whirlpool of rotating air is created around a spinning baseball. The ball’s velocity is enhanced on the side where its rotation is in the same direction as the wind stream in which it is traveling. On the opposite side of the ball, where the whirlpool and wind stream are opposed, the ball’s velocity is slowed, due to the Bernoulli effect which maintains that wherever fluid velocity is slower its pressure is higher.

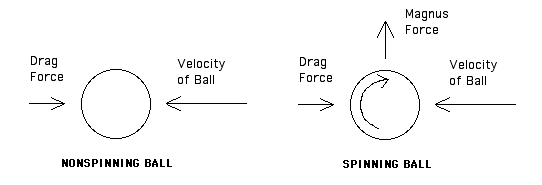
The unbalanced force on the ball due to its rotation creates curvature in its path which can be as much as the width of the home plate. This is not the only pitch which takes advantage of physical principles to fool an unsuspecting batter, though.

        While a curve ball may rotate seven to sixteen times on its course to home plate, an effective knuckle ball should rotate not even once, to obtain deflection of its trajectory by more than a foot (Armenti, 1992, p. 55). The knuckle ball’s motion can be explained in basic terms very easily. Due to its lack of rotation, the baseball’s strings, being asymmetrical rough surfaces, give rise to unusual lift forces and an asymmetrical distribution of velocity about the ball. This causes the ball to fly through the air in an erratic fashion, unaffected by the speed of the pitch. The pitcher craftily challenges the batter to compensate.

        The batter, stepping up to the plate and staring the pitcher in the eye, has more to worry about than the Magnus effect or asymmetrical velocity dispersal on the pitch. This solid athlete must first carefully choose his bat’s starting angle and position before the ball is pitched. During the half second that the ball travels through the air, he must choose the bat’s velocity and acceleration in three dimensions, timing those motions perfectly to meet the ball within the 10 millisecond time frame it is over the plate. In other words, a timing variance of 10 ms means the difference between a ball hit straight over second base and a ball fouled over first or third base. Another example shows how precise this athlete must be. A slight miscalculation of one millimeter in the vertical coordinate during the 1.5 ms the ball was in contact with his bat (Plagenhoef, 1971, p.71) left the batter on the losing side in the decision for the 1962 world championship (Armenti, 1992, p. 29). All of these assessments must be held off until the last possible moment, in order to gather in as much information about the trajectory of the approaching pitch as possible. As if this didn’t seem enough to defy the laws of probability if not biology, the batter is required to do this while under a mental siege of distractions such as fans booing, risk of personal injury, and a sense of individual responsibility. Maybe this time the astute batter will judge and calculate correctly enough to hit a home run.

        Assuming the batter connects with the ball, the ball is compressed on the bat and rebounds with a certain force which is a set standard in the major leagues, relative to the pitch’s and bat’s velocities. Balls must have a coefficient of restitution of .514 to .578, a measurement of how "lively" a ball rebounds (Adair, 1990, p. 67). This means a typical baseball leaves a bat with only 35% of its original energy. The variation between balls used in the major leagues today generally means that any home run hit approximately 400 feet will deviate about four feet as a result of balls’ different restitutions.

        During the moment after the ball has contacted the bat, the bat is set into a vibrating motion. An experiment was done a few years ago which compared a ball hitting one bat held by a strong clamp and a ball hitting another that was freely suspended. The clamped bat demonstrated oscillation with a node only at the clamp, called "diving board" oscillation, while the freely suspended bat oscillated at two nodes midway up its length. Comparing these measurements to how a bat behaved when held with two hands, it was found that when at the plate, the bat tended to behave more like a freely suspended object in its oscillations. The relative tightness with which the bat was held only dampened the vibrations slightly, not changing their fundamental oscillation mode. The results of this unverified experiment suggest that the grip of a batter has no effect on the ball’s velocity when it is hit. A tight grip only serves to help control the bat’s position until the moment of impact.

        Once the ball has collided with the bat at the ideal position and has been launched into the air, the nearest outfielder unconsciously calls on his reliable knowledge of physics to track the fly ball into his mitt. Close observation has revealed the method with which an outfielder judges where he should stand to receive the fly ball. At the beginning of the ball’s trajectory, the baseball player follows the ball with his head, matching the tilting of his head to the angular acceleration of the ball. If the acceleration is negative, the fielder knows he should run inward to make the catch. If he finds the angular acceleration to be positive, he runs backward. Finally, an angular acceleration of nearly zero indicates he is approximately in the right position to catch it. In the later stages of flight, though, the fielder judges the incoming ball using a different method, all learned as a result of practice and trial-and-error. As the ball approaches, he notes its perpendicular velocity component and watches as he runs until the component is zero, at which time the ball has reached his glove. Under physical scrutiny, the complexity of catching a routine fly ball is unveiled.

        Baseball, a sport of slow activity one second and fast-moving fly balls another, holds many secrets in physics. Though it has been America’s pastime since before the turn of the century, physicists still do not understand every process which takes place during those frequent games at the stadium. The pitcher tries to use the Magnus effect to his advantage. If the batter carefully executes the necessary calculations for his swing, as was shown above, he might hit the ball out of the stadium. However, he discovers that he doesn’t have the energy to hit the ball at the required speed of 75 mph (Adair, 1990, p. 74). Sixty-five percent of the ball’s energy is wasted as it collides with the bat and leaves the bat oscillating in the player’s hands. An outfielder watches the ball rise into the air and notes the ball’s change in velocity as it falls directly into his glove, and he wraps up the game’s last inning.

Armenti, Angelo, Jr. The Physics of Sports. New York, American Institute of Physics, 1992.

Plagenhoef, S. Patterns of Human Motion. Englewood Cliffs, New Jersey, Prentice-Hall, 1971.

Watts, Robert G. and A. Terry Bahill. Keep your Eye on the Ball. New York, W. H. Freeman and Company, 1990.

About this paper

Please excuse any writing mistakes I made in this paper. I wrote this as a freshman at the University of Toledo, Ohio, in March 1994, as an assignment for my first of three physics courses. Like most of my papers, I wrote the majority of it the night before it was due, between 2 a.m. and the start of class at 11 a.m. on Monday. The rest of that day of torture I drifted in and out of sleep during my classes, each seemingly hours long, and I even found myself writing jibberish in my notebook. I didn't think that could actually happen to someone. I wrote in my journal on May 23, "I would look down at my notes and read strange words or nonsense... keeping on track by copying exactly what was on the board. I couldn't understand what was going on..." So, like I said, it was a long time ago and I was up late so please don't blame me for my awkward writing style!

This paper is available on my web site, located at: http://www.teresi.us/writing

Please notify me if you would like to re-distribute this paper. I would be glad to hear it!